Numpy in Python

Main Object of NumPy:

NumPy's primary data structure is a homogeneous multidimensional array. This means it's an array where all elements are of the same data type, typically numbers. These arrays can have multiple dimensions, like one-dimensional sequences (lists of numbers) or two-dimensional tables (spreadsheets of numbers). Each element in the array is uniquely identified by a tuple of positive integers called an index.

Description:

NumPy's multidimensional arrays provide a powerful and efficient way to store and manipulate large datasets in Python. They are widely used in scientific computing, data analysis, and machine learning due to their flexibility and performance.

Key Points:

• Homogeneous: All elements have the same data type.
• Multidimensional: Can have multiple dimensions (1D, 2D, 3D, etc.).
• Indexed: Elements are accessed using tuples of positive integers.

import numpy as np

Importing numpy under the alias np has already become a generally accepted, tacit agreement, one could say, a tradition.

Now we can proceed to examples. There are quite a few ways to create NumPy arrays, but we will start with the most trivial one - creating an array from a manually filled Python list:

a = np.array([11, 22, 33, 44, 55, 66, 77, 88, 99])
print(type(a))
a

<class 'numpy.ndarray'>

array([11, 22, 33, 44, 55, 66, 77, 88, 99])

Now we have a one-dimensional array, i.e., it has only one axis along which its elements are indexed.

a[2]

33

The expression a[[7, 0, 3, 3, 3, 0, 7]] demonstrates advanced indexing in NumPy. Here's a detailed description: Description of NumPy Advanced Indexing

Advanced Indexing: This form of indexing allows you to access multiple elements of an array simultaneously using an array of indices.

Breakdown of the Expression

a: This is the original NumPy array from which you want to extract elements.
[7, 0, 3, 3, 3, 0, 7]: This is a list of indices you are using to index into array a.

What Happens

Index List: The list [7, 0, 3, 3, 3, 0, 7] specifies the positions of the elements in the array a that you want to extract.
Extraction: NumPy will use each value in the list as an index to pull corresponding elements from the array a.

Example

If a is an array like a = np.array([10, 20, 30, 40, 50, 60, 70, 80]), then:

a[7] corresponds to 80
a[0] corresponds to 10
a[3] corresponds to 40

So, a[[7, 0, 3, 3, 3, 0, 7]] will result in a new array [80, 10, 40, 40, 40, 10, 80]. Summary

Advanced indexing with arrays or lists in NumPy allows for powerful and flexible data selection capabilities, enabling extraction of multiple elements from an array based on specific index positions provided in another array or list.

a[[7, 0, 3, 3, 3, 0, 7]]

array([88, 11, 44, 44, 44, 11, 88])

Instead of a single index, an entire list of indices is specified. For example, now instead of an index, we will specify a logical expression:

a[a > 50]

array([55, 66, 77, 88, 99])

Demonstration of NumPy's advanced array indexing capabilities.

Vectorized calculations:

2*a + 10

array([ 32,  54,  76,  98, 120, 142, 164, 186, 208])

np.sin(a)**2 + np.cos(a)**2

array([1., 1., 1., 1., 1., 1., 1., 1., 1.])

Vectorized means that all arithmetic operations and mathematical functions are performed simultaneously on all elements of the arrays. This, in turn, means that there is no need to perform calculations in a loop.

Two-dimensional arrays:

a = np.arange(12)
a

array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11])

a = a.reshape(3, 4)
a

array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11]])

Now we have created an array using the np.arange() function, which is very similar to the range() function in Python.

Then, we changed the shape of the array using the reshape() method, which means we could have actually created this array with a single command:

a = np.arange(12).reshape(3, 4)
a

array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11]])

Visually, this array looks as follows:

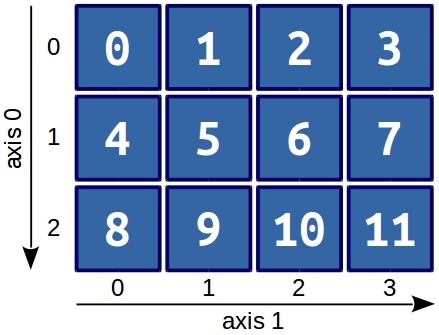
Looking at the picture, it becomes clear that the first axis (and index accordingly) is the rows, and the second axis is the columns. That is, to get element 9, you can use a simple command:

a[2][1]    

9

Broadcasting arrays.

In this example, without any loops, we multiplied each column from array a by the corresponding element from array b.

That is, we broadcasted (to some extent, you could say stretched) array b over array a.

b = [2, 3, 4, 5]
a * b

array([[ 0,  3,  8, 15],
       [ 8, 15, 24, 35],
       [16, 27, 40, 55]])

We can do the same with each row of array a:

c = [[10],
     [20],
     [30]]
a + c

array([[10, 11, 12, 13],
       [24, 25, 26, 27],
       [38, 39, 40, 41]])

In this case, we simply added array c, a column array, to array a.

When working with two-dimensional or three-dimensional arrays, especially with arrays of higher dimensions, it becomes very important to conveniently work with elements of the array that are located along its individual dimensions - its axes.

For example, we have a two-dimensional array and we want to find its minimum elements by rows and columns.

To start, let's create an array of random numbers and, for our convenience, let these numbers be integers:

a = np.random.randint(0, 15, size=(4, 6))
a

array([[10,  2, 14,  7, 11,  3],
       [ 3,  8, 12, 13,  0,  0],
       [ 4,  1, 14,  9, 14, 13],
       [12,  1,  9,  5,  1, 12]])

The minimum element in this array is:

a.min()

0

And here are the minimum elements by columns and rows: minimum elements by rows

a.min(axis=0)    #  minimum elements by columns

array([3, 1, 9, 5, 0, 0])

a.min(axis=1)    #  minimum elements by rows

array([2, 0, 1, 1])

This behavior is built into almost all NumPy functions and methods:

a.mean(axis=0)       #  average value by columns

array([ 7.25,  3.  , 12.25,  8.5 ,  6.5 ,  7.  ])

np.std(a, axis=1)    #  standard deviation by rows

array([4.29793232, 5.32290647, 5.07991688, 4.64279609])

What about computations, their speed, and memory usage?

For example, let's create a three-dimensional array.

a = np.arange(48).reshape(4, 3, 4)
a

array([[[ 0,  1,  2,  3],
        [ 4,  5,  6,  7],
        [ 8,  9, 10, 11]],

       [[12, 13, 14, 15],
        [16, 17, 18, 19],
        [20, 21, 22, 23]],

       [[24, 25, 26, 27],
        [28, 29, 30, 31],
        [32, 33, 34, 35]],

       [[36, 37, 38, 39],
        [40, 41, 42, 43],
        [44, 45, 46, 47]]])

Why specifically three-dimensional?

In reality, the world is not limited to tables, vectors, and matrices.

There are also tensors, quaternions, octaves. Some data is much more conveniently represented in three-dimensional and four-dimensional forms:

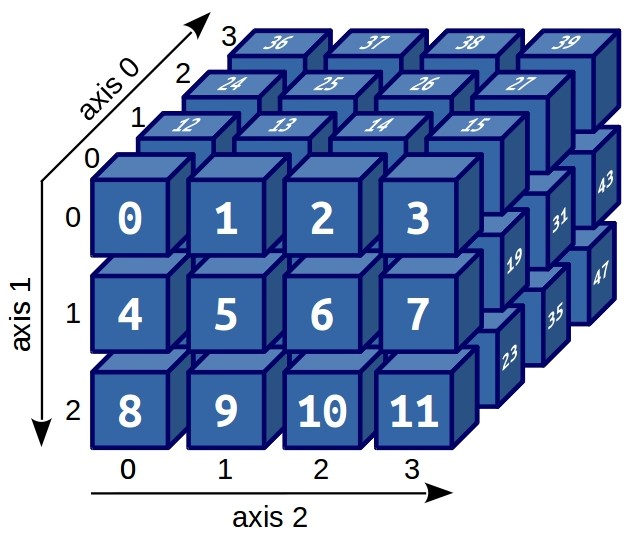
Visualization (and good imagination) allows you to immediately guess how indexing of three-dimensional arrays is arranged. For example, if we need to extract the number 31 from this array, it is enough to execute:

a[2][1][3]   

31

Indeed, arrays have a number of important attributes. For example, the number of axes of an array (its dimensionality), which, when working with very large arrays, is not always easy to see: The array a is indeed three-dimensional.

a.ndim

3

The array a is indeed three-dimensional.

But sometimes it becomes interesting to know how large the array actually is. For example, what is its shape, i.e., how many elements are along each axis? The method ndarray.shape allows us to answer this:

a.shape

(4, 3, 4)

The ndarray.size method simply returns the total number of elements in the array:

a.size

48

Another question that may arise is - how much memory does our array occupy?

Sometimes it even becomes a question of whether the resulting array after all calculations will fit into the RAM.

To answer this, we need to know the "size" in bytes of one element of the array:

a.itemsize    #  equivalent ndarray.dtype.itemsize

8

ndarray.itemsize returns the size of the element in bytes.

Now we can find out how much our array “weighs”:

a.size * a.itemsize

384

In total - 384 bytes. In fact, the memory size occupied by the array depends not only on the number of elements in it but also on the data type used:

a.dtype

dtype('int64')

dtype('int64') means that an integer data type is used, where 64 bits of memory are allocated to store one number.

But if we perform any calculations with the array, the data type may change:

b = a/3.14
b

array([[[ 0.        ,  0.31847134,  0.63694268,  0.95541401],
        [ 1.27388535,  1.59235669,  1.91082803,  2.22929936],
        [ 2.5477707 ,  2.86624204,  3.18471338,  3.50318471]],

       [[ 3.82165605,  4.14012739,  4.45859873,  4.77707006],
        [ 5.0955414 ,  5.41401274,  5.73248408,  6.05095541],
        [ 6.36942675,  6.68789809,  7.00636943,  7.32484076]],

       [[ 7.6433121 ,  7.96178344,  8.28025478,  8.59872611],
        [ 8.91719745,  9.23566879,  9.55414013,  9.87261146],
        [10.1910828 , 10.50955414, 10.82802548, 11.14649682]],

       [[11.46496815, 11.78343949, 12.10191083, 12.42038217],
        [12.7388535 , 13.05732484, 13.37579618, 13.69426752],
        [14.01273885, 14.33121019, 14.64968153, 14.96815287]]])

b.dtype

dtype('float64')

Now we have another array - array b and its data type is 'float64' - floating-point numbers (numbers with decimal points) with a length of 64 bits.

And its size is:

b.size * b.itemsize

384

To create arrays in NumPy

And so, an array can be created from a regular Python list or tuple using the array() function.

The type of the resulting array depends on the type of the elements in the sequence:

import numpy as np

a = np.array([1, 2, 3])
a

array([1, 2, 3])

a.dtype

dtype('int64')

a = np.array([1.1, 2.2, 3.3])
a

array([1.1, 2.2, 3.3])

a.dtype

dtype('float64')

a = np.array([1 + 2j, 2 + 3j])
a

array([1.+2.j, 2.+3.j])

a.dtype

dtype('complex128')

The array() function converts sequences of sequences into two-dimensional arrays, and sequences of sequences of sequences into three-dimensional arrays.

Thus, the nesting level of the original sequence determines the dimensionality of the resulting array.

a = np.array([[2, 4], [6, 8], [10, 12]])
a

array([[ 2,  4],
       [ 6,  8],
       [10, 12]])

b = np.array([[[1, 2], [3, 4]],
              [[5, 6], [7, 8]],
              [[9, 10], [11, 12]]])
b

array([[[ 1,  2],
        [ 3,  4]],

       [[ 5,  6],
        [ 7,  8]],

       [[ 9, 10],
        [11, 12]]])

a.ndim    #  Number of array axes

2

b.ndim    #  Number of array axes

3

Very often, there is a task to create an array of a certain size, and it doesn't matter what the array is filled with.

In this case, you can use loops or list (tuple) comprehensions, but NumPy offers faster and less resource-intensive filler functions for such cases.

The zeros() function fills the array with zeros, the ones() function fills it with ones, and the empty() function fills it with random numbers that depend on the state of the memory.

By default, the type of the created array is float64.

np.zeros((3,3))

array([[0., 0., 0.],
       [0., 0., 0.],
       [0., 0., 0.]])

np.ones((3,3))

array([[1., 1., 1.],
       [1., 1., 1.],
       [1., 1., 1.]])

np.ones((3,3), dtype=complex)  #  Можно изменить тип массива

array([[1.+0.j, 1.+0.j, 1.+0.j],
       [1.+0.j, 1.+0.j, 1.+0.j],
       [1.+0.j, 1.+0.j, 1.+0.j]])

np.empty([3, 3])

array([[0., 0., 0.],
       [0., 0., 0.],
       [0., 0., 0.]])

To create sequences of numbers, NumPy provides the arange() function, which returns one-dimensional arrays:

np.arange(10)    

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

np.arange(10, 20)    

array([10, 11, 12, 13, 14, 15, 16, 17, 18, 19])

np.arange(20, 100, 10)    

array([20, 30, 40, 50, 60, 70, 80, 90])

np.arange(0, 1, 0.1)    

array([0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9])

If the arange() function is used with arguments of type float, predicting the number of elements in the returned array is not so simple.

More often, there is a need to specify not the step size of numbers in the range, but the number of numbers in the given range.

The linspace() function, like arange(), takes three arguments, but the third argument specifies the number of numbers in the range.

np.linspace(0, 1, 5)

array([0.  , 0.25, 0.5 , 0.75, 1.  ])

np.linspace(0, 1, 7)

array([0.        , 0.16666667, 0.33333333, 0.5       , 0.66666667,
       0.83333333, 1.        ])

np.linspace(10, 100, 5)

array([ 10. ,  32.5,  55. ,  77.5, 100. ])

The linspace() function is also convenient because it can be used to compute function values at a given set of points:

x = np.linspace(0, 2*np.pi, 10)
x

array([0.        , 0.6981317 , 1.3962634 , 2.0943951 , 2.7925268 ,
       3.4906585 , 4.1887902 , 4.88692191, 5.58505361, 6.28318531])

y1 = np.sin(x)
y1

array([ 0.00000000e+00,  6.42787610e-01,  9.84807753e-01,  8.66025404e-01,
        3.42020143e-01, -3.42020143e-01, -8.66025404e-01, -9.84807753e-01,
       -6.42787610e-01, -2.44929360e-16])

y2 = np.cos(x)
y2

array([ 1.        ,  0.76604444,  0.17364818, -0.5       , -0.93969262,
       -0.93969262, -0.5       ,  0.17364818,  0.76604444,  1.        ])

Output of arrays to the screen

To quickly understand the examples of printing arrays, we will use the ndarray.reshape() method, which allows changing the dimensions of arrays.

One-dimensional arrays in NumPy are printed as rows:

a = np.arange(10)                     #  One-dimensional array
print(a)

[0 1 2 3 4 5 6 7 8 9]

Two-dimensional arrays are printed as matrices:

b = np.arange(16).reshape(4, 4)       #  Two-dimensional array
print(b)

[[ 0  1  2  3]
 [ 4  5  6  7]
 [ 8  9 10 11]
 [12 13 14 15]]

Three-dimensional arrays are printed as a list of matrices separated by an empty line:

c = np.arange(30).reshape(5, 2, 3)    #  Three-dimensional array
print(c)

[[[ 0  1  2]
  [ 3  4  5]]

 [[ 6  7  8]
  [ 9 10 11]]

 [[12 13 14]
  [15 16 17]]

 [[18 19 20]
  [21 22 23]]

 [[24 25 26]
  [27 28 29]]]

You can experiment with printing arrays of higher dimensions, and you will find that it is quite easy to navigate.

In the case of a very large array (more than 1000 elements), NumPy prints only the beginning and end of the array, replacing the middle part with an ellipsis.

print(np.arange(1001))

[   0    1    2 ...  998  999 1000]

print(np.arange(1000000))

[     0      1      2 ... 999997 999998 999999]

print(np.arange(1000000).reshape(1000,1000))

[[     0      1      2 ...    997    998    999]
 [  1000   1001   1002 ...   1997   1998   1999]
 [  2000   2001   2002 ...   2997   2998   2999]
 ...
 [997000 997001 997002 ... 997997 997998 997999]
 [998000 998001 998002 ... 998997 998998 998999]
 [999000 999001 999002 ... 999997 999998 999999]]

If it is necessary to print the entire array, this printing behavior can be changed using the set_printoptions() function.

np.set_printoptions(threshold=np.nan)

File input and output of arrays

When doing scientific computations, you obtain results that must be saved.

The most reliable way to store them is by saving the arrays with the results to a file, as they are easy to store and transfer.

For these needs, NumPy provides very convenient tools that allow loading and saving arrays to files in various formats, as well as compressing them, which is necessary for large arrays.

Binary files NumPy .npy, .npz

NumPy has two native file formats: .npy for storing arrays without compression and .npz for pre-compressing arrays.

If the arrays that need to be saved are small, you can use the numpy.save() function. In the simplest case, this function takes only two arguments: the name of the file to which the array will be saved and the name of the array to be saved. However, it should be noted that the file will be saved in the directory where the Python script is being executed or in the specified location:

import numpy as np

a = np.arange(12).reshape(3, 4)
a

array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11]])

b = np.arange(16).reshape(4, 4)
b

array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11],
       [12, 13, 14, 15]])

#  The file will be saved in the same folder as the executing script
np.save('example_1', a)

After the array is saved, it can be loaded from the file using the numpy.load() function, specifying the filename as a string if it is in the same directory as the executing Python script, or the path to it if it is located elsewhere.

import numpy as np

a = np.load('example_1.npy')
a

array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11]])

.npy files are convenient for storing a single array. If multiple arrays need to be saved in one file, you should use the numpy.savez() function, which will save them in an uncompressed form in a .npz format NumPy file.

a = np.array([1, 2, 3])
b = np.array([[1, 1], [0, 0]])
c = np.array([[1], [2], [3]])

np.savez('example_2', a, b, c)

After saving arrays to a .npz file, they can be loaded using the familiar numpy.load() function. However, the names of the arrays have now changed from a, b, and c to arr_0, arr_1, and arr_2 respectively:

ex_2 = np.load('example_2.npz')

ex_2.files

['arr_0', 'arr_1', 'arr_2']

ex_2['arr_0']

array([1, 2, 3])

ex_2['arr_1']

array([[1, 1],
       [0, 0]])

ex_2['arr_2']

array([[1],
       [2],
       [3]])

To preserve the original names of arrays when saving them, you need to specify them as keys in the numpy.savez() function:

np.savez('example_2', a=a, b=b, c=c)

ex_2 = np.load('example_2.npz')

ex_2.files

['a', 'b', 'c']

ex_2['a']

array([1, 2, 3])

For very large arrays, you can use the numpy.savez_compressed() function.

a = np.arange(100000)
a

array([    0,     1,     2, ..., 99997, 99998, 99999])

#  The file example_3.npy occupies 400 KB on disk:
np.save('example_3', a)

#  The file example_3.npynpz occupies only 139 KB on disk:
np.savez_compressed('example_3', a)

In reality, .npz files are simply zip archives that contain individual .npy files for each array.

After a file has been saved using the numpy.savez_compressed() function, it can also be easily loaded using the numpy.load() function.

ex_3 = np.load('example_3.npz')
ex_3.files

['arr_0']

ex_3['arr_0']

array([    0,     1,     2, ..., 99997, 99998, 99999])

NumPy: the absolute basics for beginners

https://numpy.org/doc/stable/user/absolute_beginners.html

NumPy fundamentals

https://numpy.org/doc/stable/user/basics.creation.html

100 numpy exercises

https://github.com/rougier/numpy-100